This post is part of a series. If you wish to support my work you can purchase the PDF book on gumroad.
This project uses Elm version 0.19
- Part 1 - Introduction (this post)
- Part 2 - Project Setup
- Part 3 - Add CSS
- Part 4 - Basic Operations
- Part 5 - Adding Decimal Support
- Part 6 - Supporting Negative Numbers
- Part 7 - Add Dirty State
- Part 8 - Support Keypad Input
- Part 9 - Combination Key Input
- Part 10 - Testing
- Part 11 - Netlify Deployment
Final project demo
- Demo link: https://elm-calculator.netlify.com
- Git Repo: https://gitlab.com/pianomanfrazier/elm-calculator
Who is this book for?
I wrote this book because I found it difficult to recommend tutorials to those wanting to start using Elm. Beginners might feel intimidated by the new syntax and the non-component way of doing things. If you are coming from React or Vue things will look a bit different. There are no components. Only functions.
After dabbling in Elm for a while I knew I wanted to use it in a larger project but I didn't know where to get started. There seemed like I had to learn so much it was easy to get discouraged. I kept coming back to Elm hoping things would click.
This is the book I wish I had when starting to learn Elm.
Hopefully this will save you time and help you get past the rough patches when starting out with Elm.
Learn by doing
Whenever I learn something new, I learn best by actually doing it. If you want to learn a new computer language pick a project and just go for it.
This book is an attempt to guide a beginner through building something non-trivial in Elm. It will be very light on the theory and focus on building stuff.
What will be covered?
- Elm's type system
- CSS with external style sheet
- elm-live development server
- custom keyboard input events
- key combo events (like alt-shift-delete)
- testing with elm-program-test and elm-test
- Browser.sandbox vs Browser.element vs Browser.document
- refactoring an Elm application
- deployment the application with Netlify
Who am I?
I have been working as a software engineer for about 4 years and I like to program mostly for the web. In my day to day work I use Vue.js a lot (still trying to convince my co-workers to try Elm, hence this book).
I have experience writing backends in Node.js, Python, and Java. I also love static site generators like Hugo and 11ty.
I love to learn new things and try new things out. On a whim I decided to try Elm because it looked so different from what I was used to. I tried it and I was pleasantly surprised. If I am going to write something complex in the browser Elm is my first choice.
Provided resources
Provided with each chapter are the following:
- the git repo with the result of the chapter - https://gitlab.com/pianomanfrazier/elm-calculator
- a link to the ellie-app version of the code - https://ellie-app.com/72nScWrSMfVa1
- a link to the diff - https://gitlab.com/pianomanfrazier/elm-calculator/-/compare/v0.1...v0.2
What is ellie app?
Ellie app is an online environment to code in Elm online. There is no setup involved. It is similar to CodePen or JSbin.
Try it out at https://ellie-app.com.
What are we going to build?
We are going to build a calculator. Since they are easier to program, we are going to build a Reverse Polish Notation (RPN) calculator.
Here is what it will look like when it is done.
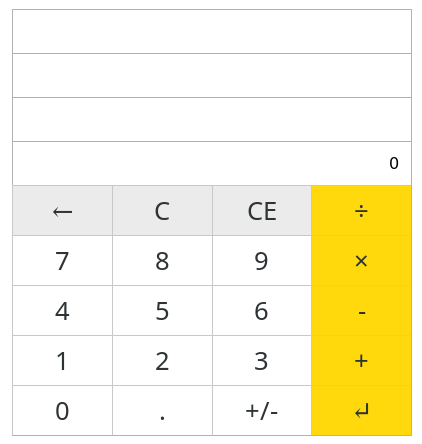
Go to https://elm-calculator.netlify.com for a demo of the finished calculator.
An RPN Calculator is easier to program because all operations work on the stack. Let's briefly explore the stack and how it works with our calculator.
The Stack
A stack is a data structure that has two operations: push and pop. Similar to a stack of plates, you can push onto the stack by placing things on top. Likewise you take things off the stack by popping off the top. Another name for this is LIFO (last in first out).
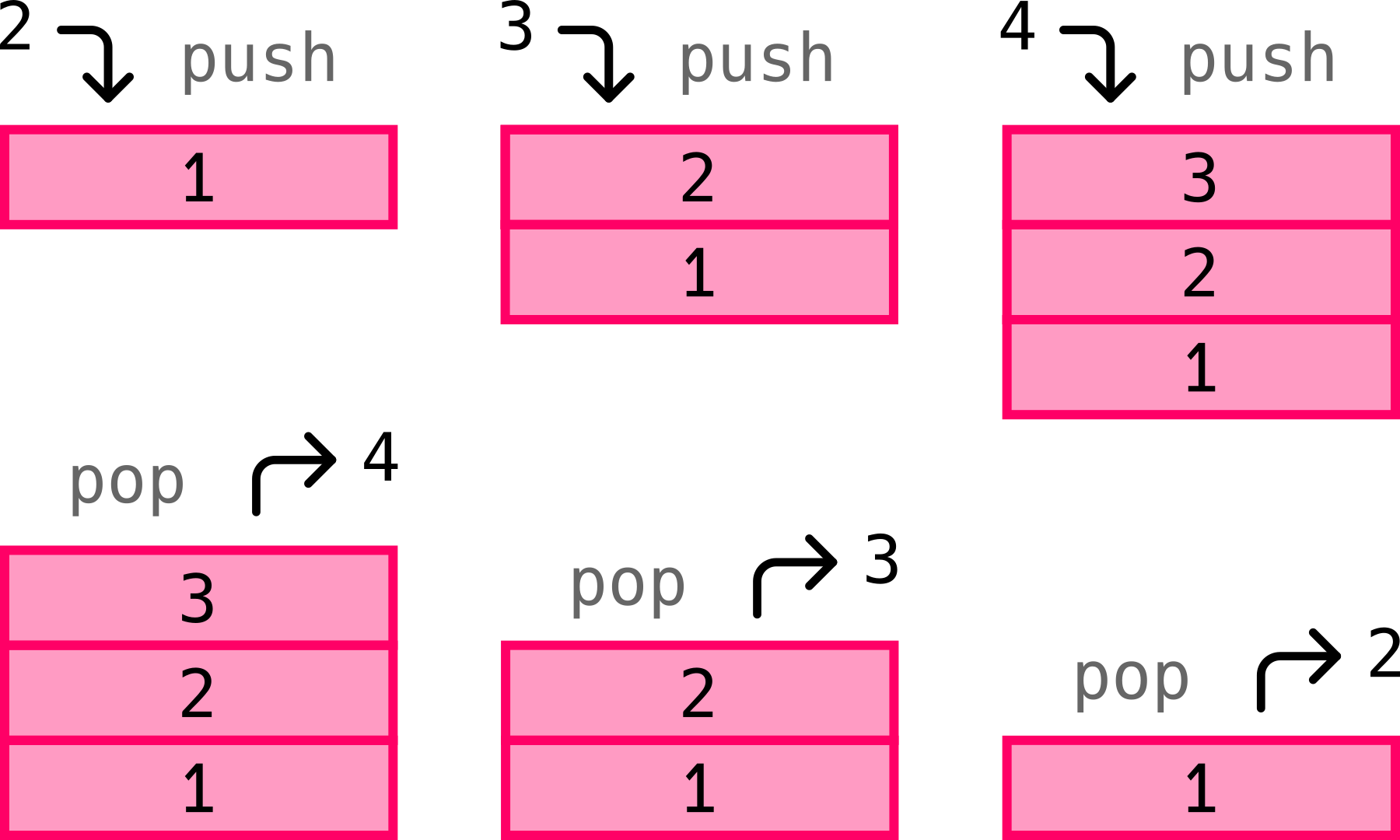
For our calculator, we push numbers onto the stack. To pop items off we perform operations on the numbers of the stack. The operators "+", "-", "÷", and "×" need to operate on two numbers, so these operators will pop 2 numbers off the stack, operate on them and then push the result back onto the stack.
For example we push "1" and then "2" onto the stack. Then press the "+" operator. This pops "1" and "2" off the stack, operates on them and then pushes "3" back onto the stack.

When we do this on an RPN calculator the stack is usually shown up-side-down. The new numbers keep pushing the stack upward.
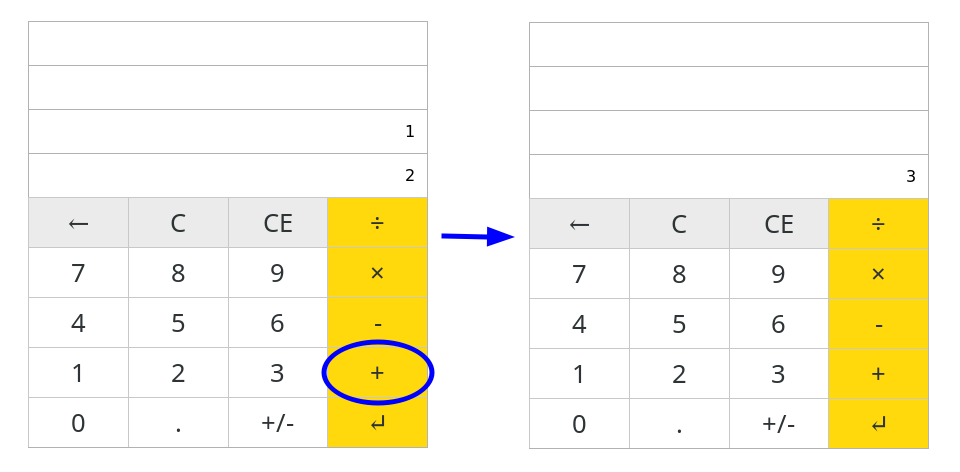
Why is a traditional calculator harder?
The alternative would be to parse a computation string like 1 + 2. This is what we call "infix" notation, the operator is in between the operands (the numbers). RPN notation is called "postfix" notation, "1 2 +", meaning the operation comes after the operands.
"1 + 2" would be trivial parse. But what about order of operations and parenthesis like in "3 × (4 + 6) ÷ 3 + 4 × 5"?
Let's avoid dealing with order of operations and just do postfix notation instead.
Binary and Syntax Trees
Disclaimer: You really can skip this section. I promised light on theory. This section is a bit heavy on theory and not totally necessary to build the project.
Say you really want to program a normal calculator with parenthesis and order of operations. It will be helpful to understand something about tree structures.
If you type "1 + 2" into your calculator. The calculator needs to know it's a valid expression in order to compute it. What if you type in something bogus like "1 + 2 +" and then press enter?

My calculator reported "ERR:SYNTAX". How did it know that? It needed to parse the whole equation and then figure out it was invalid.
After we parse the equation, we can represent the math equation as a tree structure.
This tree structure is called a syntax tree. And in the case of the "+" operator the tree is also a binary tree because each node (the operators) has two leaves or childern (the operands).
Let's take our two examples above and parse them into trees.
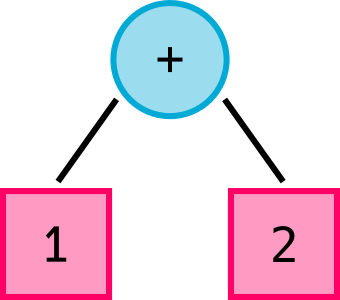
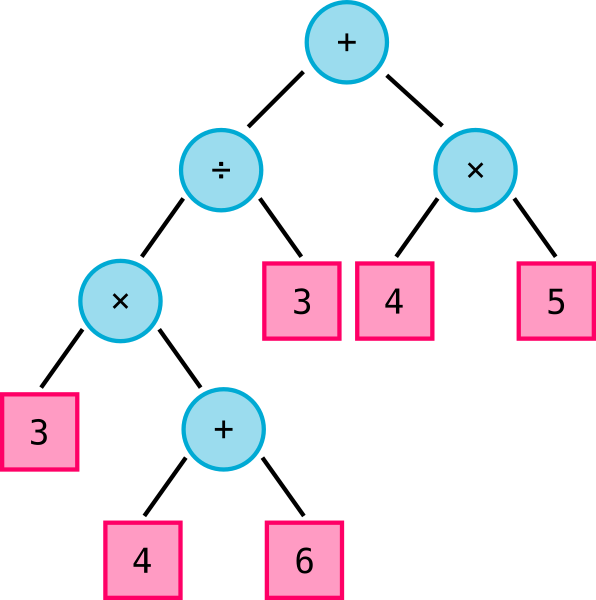
The blue circles are operators and the red squares are the operands. Each operator in these examples, requires two operands, or tree leaves, to be valid.
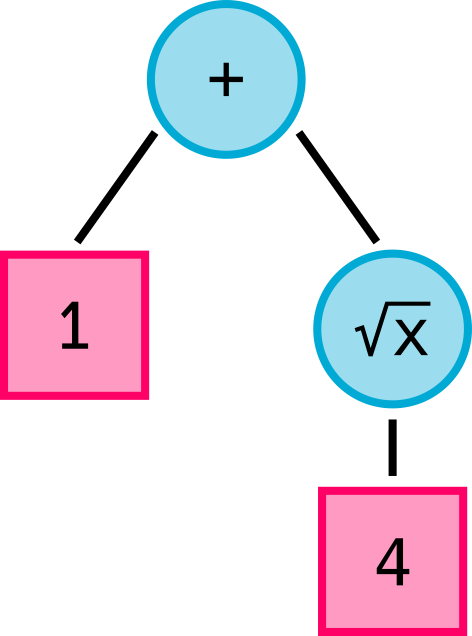
There are other operators like the square root, √x, or inverse, 1/x, that operate on only one operand. These operators would require one leaf, or child, in the tree.
Process the tree
So if we parse the equation into a valid tree, then what? We need to process the tree.
We need to collapse all the operator nodes with two children until our whole tree is processed. If you were to collapse the tree by hand it would look something like .
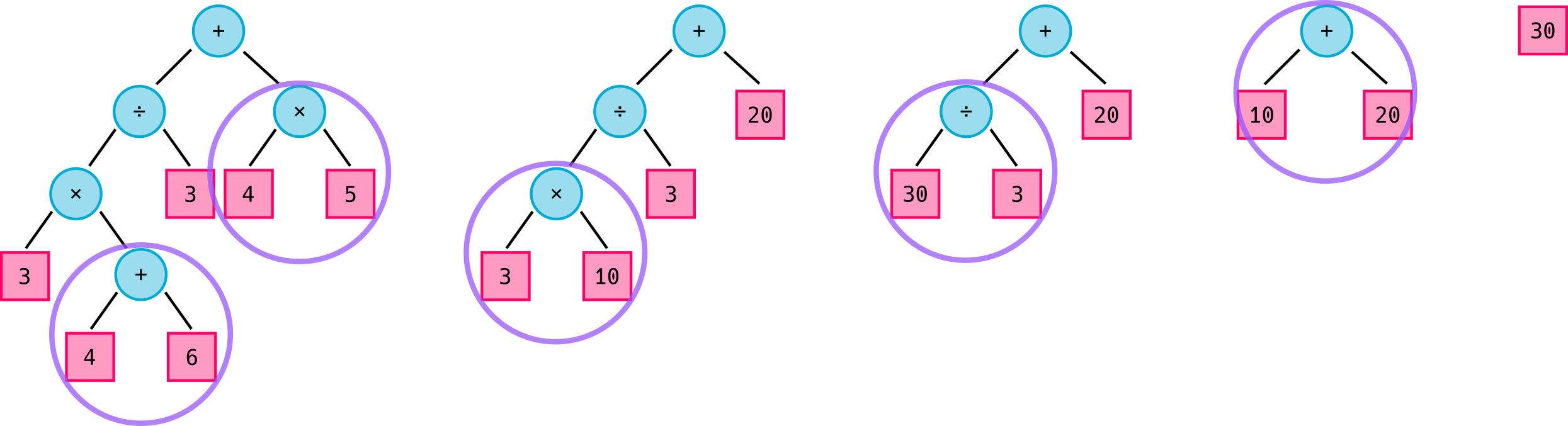
We need a more systematic way of traversing the tree. There are several ways to go through the tree but we can just use the stack just like before. This is called a post order traversal because we process the children (operands) first and then the operator.
Process tree on the stack
We already process the simple example "1 + 2" on the stack. Let's go through a more complex example to see how this is done.
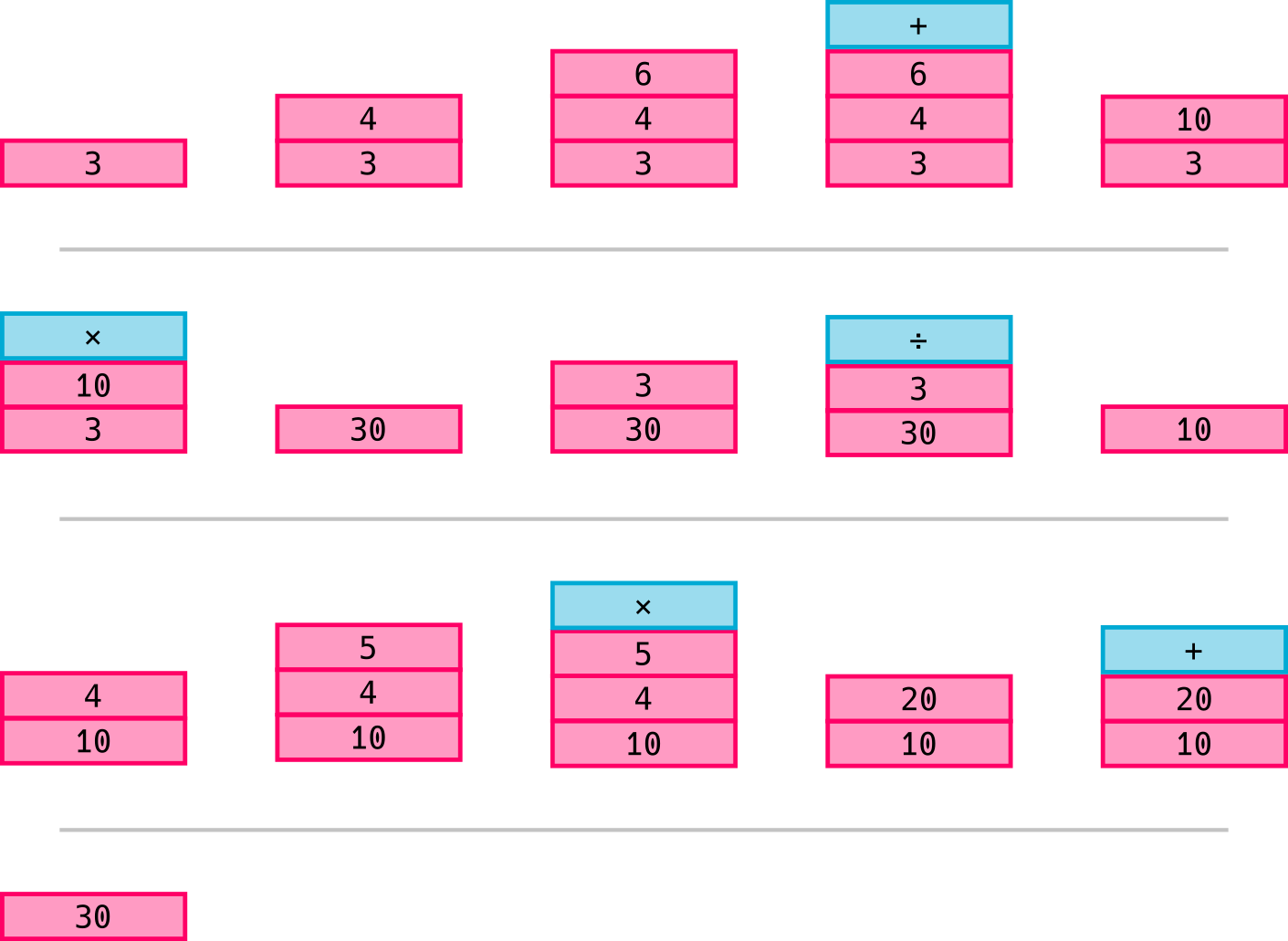
The process on the stack is similar to how we would have collapse the tree by hand. We take the bottom most thing we can compute and stick the numbers on the stack. When we get to an operator we evaluate it and stick it on the stack.
Hopefully you can see now that we can skill the parsing and building of a tree by just using the stack directly with an RPN calculator. The user won't be allowed to enter in an invalid equation.
In the next post we will setup our elm project. See you there.